 MATLAB/simulink
MATLAB/simulink MATLABで忘却係数付き逐次最小二乗法を実装する
忘却係数付き逐次最小二乗法の更新則は \begin{align}\hat{\theta}_{N} &= \hat{\theta}_{N-1} + \dfrac{P_{N-1} z_{N} }{\rho + z_{N}^{T} P_{N-1}...
 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 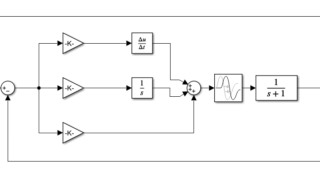 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 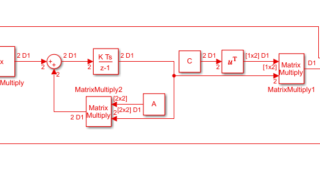 MATLAB/simulink
MATLAB/simulink 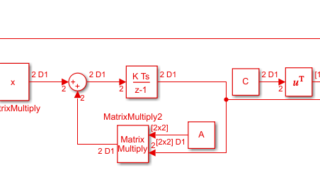 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 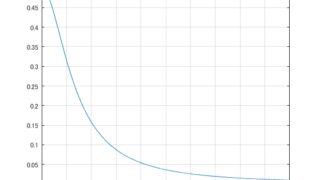 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink