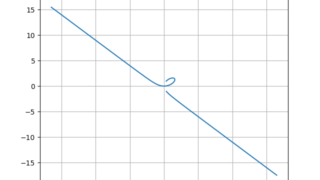
代数 Pythonでデカルトの正葉線を描く
デカルトの正葉線は\begin{align}x=\frac{3at}{1+t^3}, \hspace{5mm} y=\frac{3at^2}{1+t^3}\end{align}で表される方程式である。グラフはとなる。
代数
代数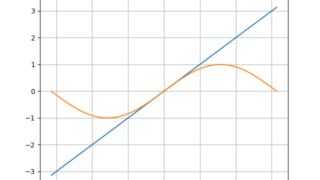 
python Pythonでxが原点周りのときのy=sin xのグラフ
\(y=\sin x\)は\(x\)が十分小さい時、\(y=x\)と近似できることが知られている。一周期分を取り出せば２つのグラフのズレはこんな感じ。たしかに小さいとよく一致している。
代数 交代行列の対角成分の性質
交代行列の対角成分は0となる。交代行列の定義\begin{align}A^{T}={}^{t} A=-A\end{align}より\begin{align}A^{T}+A\end{align}を考える。対角成分\(a_{ii}\)は交代行列...
代数 交代行列の定義
転置行列がもとの行列の\(-1\)倍となる行列\begin{align}A^{T}={}^{t} A=-A\end{align}を交代行列という。
代数 直交変換と内積の関係
直交変換において、内積の結果は不変となる。即ち\begin{align}u=Av\end{align}において\begin{align}u^{T} u &= v^{T} v \\\| u \| &= \| v \|\end{align}
代数 直交変換の定義
ベクトル\(v\)について、直交行列\(A\)との積\begin{align}u=Av\end{align}を直交変換という。
代数 直交行列の定義
次の性質を満たす正方行列\(A\)を直交行列という。\begin{align}A^{T}A = A A^{T} = E\end{align}
代数 部分分数分解のやり方 その１
部分分数分解を考える\begin{align}\frac{cx+d}{(x+a)(x+b)}=\frac{A}{x+a}+\frac{B}{x+b}\end{align}右辺を通分すれば\begin{align}\frac{cx+d}{(x...
代数 3次式の因数分解と展開に関する公式について
今回は３次式の因数分解・展開公式が実際に成り立つか確認する。まず\begin{align}x^3+y^3=(x+y)(x^2-xy+y^2)\end{align}については多項式の除法を使ってとなる。\begin{align}x^3+3x^...
C/C++/C# C++でアペリーの定理を計算する
ゼータ関数が\(s=3\)の時の結果が無理数であるという結果である。今回はC++でアペリーの定理を計算する。\begin{align}\zeta(3)=\sum_{n=1}^\infty \frac{1}{n^3}=1.2020569 \c...
代数 一次独立と一次従属
\(n\)個のベクトル\begin{align}\sum_{i=1}^{n} a_i x_i=0\end{align}について\(a_i\)以外に解が無いとき一次独立という。\(a_i\)以外に解があるとき一次従属という。
C/C++/C# Eigenで逆行列を求める
coreのほかにLUも必要。#include "../Eigen/core"#include "../Eigen/LU"あとはA.inverse()とすればいい。実行結果。-0.666667 -1.33333 1-0.666667 3.66...
C/C++/C# 行列の固有値と行列式の関係
行列の固有値の積は行列式の値と等しくなる。これをEigenで試す。実行結果固有値 (16.7075,0)(-0.905741,0) (0.198246,0)行列式-3確かめれば\begin{align}16.7075 \times (-0....
C/C++/C# Eigenで固有値と固有ベクトルを計算する
Eigenで固有値と固有ベクトルを求めるにはEigen::EigenSolver< Eigen::MatrixXf > s(A);とした後、sに対してs.eigenvalues() とすれば固有値を、s.eigenvectors()とすれば...
C/C++/C# トレースとフロベニウスノルムの関係
\(A\)と\(A\)の転地の積のトレースはフロベニウスノルムの二乗と等しくなる。つまり\begin{align}\mathrm{tr} (A A^{T}) = \mathrm{tr} (A^{T} A) = \sum_{i=1}^{n}\...
C/C++/C# トレースの性質
トレースにはつぎのようなの性質がある。\begin{align}\mathrm{tr} {A1} + \mathrm{tr}{A2} &= \mathrm{tr} ( A1+A2 ) \\a\ \mathrm{tr} {A1} &= \ma...
C/C++/C# トレースの性質 その１
トレースには次の性質がある。\begin{align}tr (A+B) = tr A + tr B\end{align} 今回はこれをC++で計算する。実行結果1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,1...
C/C++/C# C++でトレースを求める
正方行列の対角成分の和\begin{align}tr A = \sum_{i=1}^{n} a_{ii}\end{align}をトレースという。今回はこれをC++で計算する。実行結果1,2,3,4,5,6,7,8,9,15ソースコード#in...
代数 二次形式の定義
\(n\)個の変数による二次形式は\begin{align}f(x_1,x_2,\cdots,x_{n-1},x_n)=\sum_{i=1,j=1}^{n} c_{i,j} x_i x_j\end{align}\(n=2\)の時は定数\(x...
代数 行列の特異値
行列\(A\)について、その随伴行列\(A^{*}\)との積\(AA^{*}\)を考える。この時固有値\(\lambda(AA^{*})\)の平方根を\begin{align}\sigma(A)=\sqrt{AA^{*}}\end{alig...