 数学
数学 対数積分とコーシの主値
対数積分\begin{align}\mathrm{Li} (x) = \int_0^x \frac{1}{\log t} dt\end{align}は\(t=1\)で特異点を持つのでコーシの主値を使って\begin{align}\mathr...
 数学
数学  数学
数学  MATLAB/simulink
MATLAB/simulink  python
python  数学
数学  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 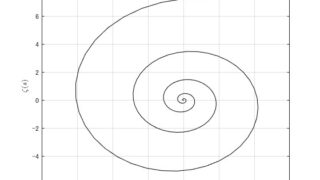 MATLAB/simulink
MATLAB/simulink 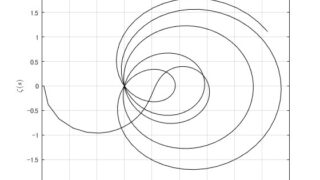 MATLAB/simulink
MATLAB/simulink 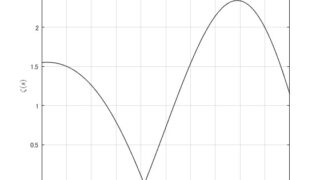 MATLAB/simulink
MATLAB/simulink 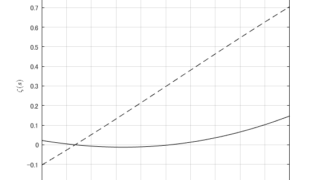 MATLAB/simulink
MATLAB/simulink  python
python  python
python  python
python  python
python  python
python