MATLABの関数を使ってゼータ関数の零点を計算する。今回はクリティカルライン上の計算結果を複素平面上にプロットした。
当然、原点との交点が
\begin{align}
\zeta(s)= \sum_{i=1}^{\infty} \frac{1}{n^s} =0
\end{align}
の点になる。
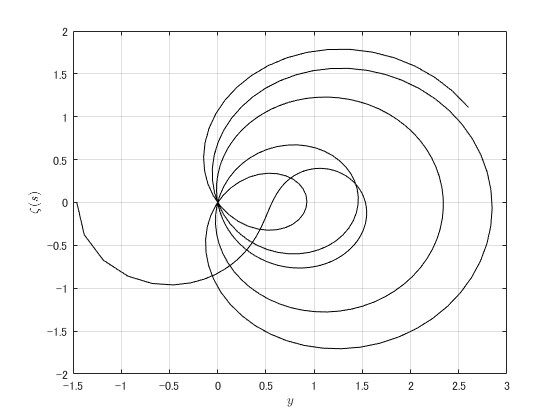
以下コード。
Nmin=0;
Nmax=35;
d=0.1;
count=1;
result=zeros(1,Nmax/d);
for y=Nmin:d:Nmax
s=1/2+y*j;
result(1,count)=zeta(s);
count=count+1;
end
fig1 = figure('name', 'ゼータ関数の特殊値');
plot(real(result),imag(result),'k-')
grid on
xlabel('$y$','Interpreter', 'latex');
ylabel('$\zeta(s)$','Interpreter', 'latex');


コメント