MATLABを使ってゼータ関数の零点を計算する。\(s\)を\(s=\frac{1}{2}+yi\)とするとゼータ関数は
\begin{align}
\zeta(s)= \sum_{i=1}^{\infty} \frac{1}{n^s}
\end{align}
となる。MATLABの関数を使って描画すれば
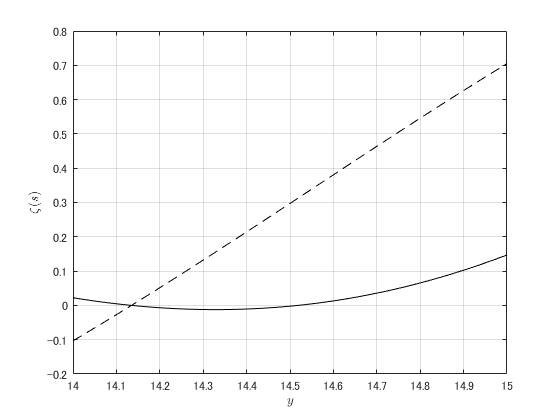
となる。\(\zeta=0\)のときに2つのグラフが交わる部分が零点。
以下コード。
Nmin=14;
Nmax=15;
d=0.001;
N=14;
n=50000;
j=sqrt(-1);
result=zeros(1,N);
y1=zeros(1,N);
count=1;
for y=Nmin:d:Nmax
s=1/2+y*j;
result(1,count)=zeta(s);
count=count+1;
end
fig2 = figure('name', 'ゼータ関数の特殊値');
plot(Nmin:d:Nmax,real(result),'k-')
hold on
plot(Nmin:d:Nmax,(imag(result)),'k--');
grid on
xlabel('$y$','Interpreter', 'latex');
ylabel('$\zeta(s)$','Interpreter', 'latex');


コメント