 C/C++/C#
C/C++/C# 秋月電子に売ってるレーザ距離センサモジュールについて
VL53L1X使用 レーザー測距センサモジュール(ToF)を買ってみた。I2Cで動作する。XSHUTとGPIO01は未接続でいい。Arduinoの場合VL53L1X用のライブラリをインストールしてサンプルプログラムを動かせば終わり。似たよう...
 C/C++/C#
C/C++/C#  python
python  python
python  python
python  python
python  python
python  MATLAB/simulink
MATLAB/simulink  python
python  MATLAB/simulink
MATLAB/simulink  python
python  python
python  MATLAB/simulink
MATLAB/simulink 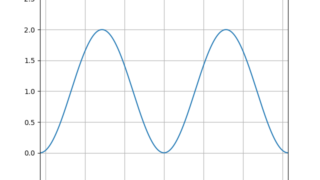 python
python 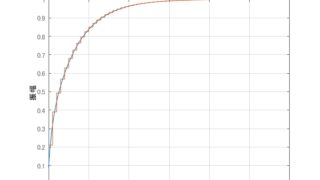 MATLAB/simulink
MATLAB/simulink  C/C++/C#
C/C++/C# 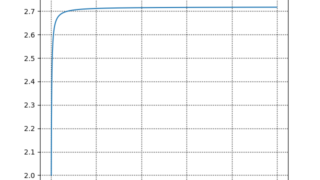 python
python 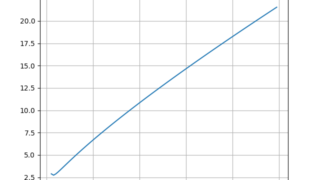 python
python 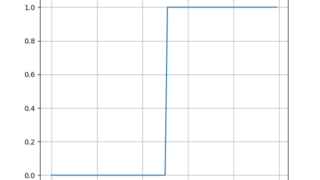 python
python  python
python 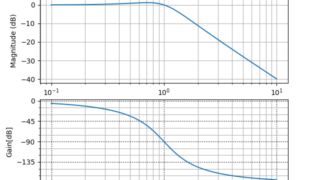 python
python