二次遅れ系の過渡応答の極大極小値

二次遅れ系の伝達関数\(G(s)\)

\begin{align}
G(s)=\dfrac{\omega_{n}^2}{s^2 + 2 \zeta \omega_{n} s+ \omega_{n}^2}
\end{align}

についての行過ぎ量を求める式は

\begin{align}
f(t) = 1 – (-1)^n e^{ -\zeta \dfrac{n \pi }{\sqrt{1-\zeta^2}} } \hspace{5mm} (n=0,1,2 \cdots)
\end{align}

を求めた。（詳細はここ）まず二次遅れ系のインディシャル応答は
\begin{align}
f(t)=1-\dfrac{e^{- \zeta \omega_{n} t} }{\sqrt{1-\zeta^2}} \sin \left (\sqrt{1-\zeta^2} \omega_{n} t + \tan^{-1} \dfrac{\sqrt{1-\zeta^2}}{\zeta} \right )
\end{align}

ここで

\begin{align}
\omega = \sqrt{1-\zeta^2} \omega_{n} \hspace{5mm} \phi=\tan^{-1} \dfrac{\sqrt{1-\zeta^2}}{\zeta}
\end{align}

とすれば

\begin{align}
f(t)=1-\dfrac{e^{- \zeta \omega_{n} t} }{\sqrt{1-\zeta^2}} \sin \left ( \omega t + \phi \right )
\end{align}

と簡潔に表すことができた。また前回の結果から応答の極大極小値の座標は

\begin{align}
\left ( \dfrac{n \pi }{\sqrt{1-\zeta^2} \omega_{n}},1 – (-1)^n e^{ -\zeta \dfrac{n \pi }{\sqrt{1-\zeta^2}} } \right )
\end{align}

となることからグラフを書けば

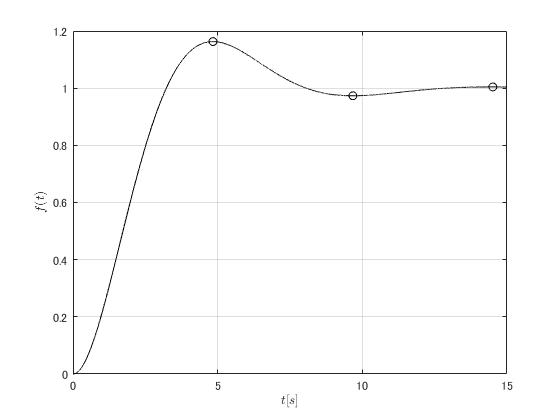
となる。グラフから明らかのように \(n=1\)のとき極大、 \(n=2\)のとき極小値をとる。