 数学
数学 直線y=ax+bの法線ベクトルを求める
\(y=ax+b\)の法線ベクトルを求める。\(f(x,y)=y-ax-b\)とおいて\begin{align}\frac{\partial f(x,y)}{\partial x}=-a \hspace{5mm} \frac{\partia...
 数学
数学 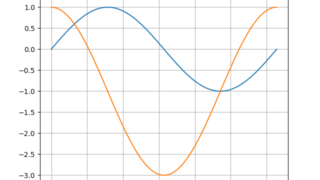 python
python 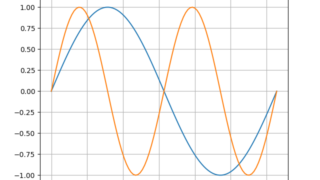 python
python 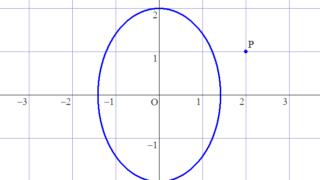 数学
数学 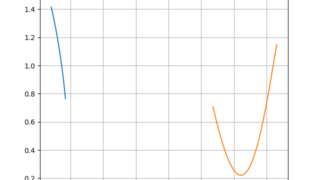 python
python 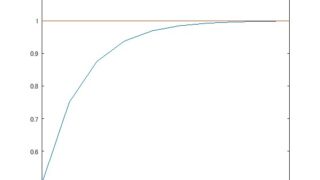 MATLAB/simulink
MATLAB/simulink 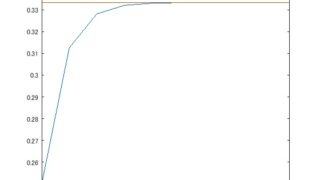 MATLAB/simulink
MATLAB/simulink  代数
代数  代数
代数  代数
代数  数学
数学  数学
数学  数学
数学  代数
代数  数学
数学 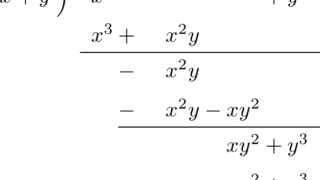 代数
代数  幾何
幾何  C/C++/C#
C/C++/C#  代数
代数  C/C++/C#
C/C++/C#