 MATLAB/simulink
MATLAB/simulink MATLABで位置ベクトルと速度ベクトルを変換するための回転行列を定義する
剛体に固定された剛体座標系と地球上に固定されたグローバル座標系を考える。いまグローバル座標系上で定義される位置ベクトルと\begin{align}\boldsymbol{\eta}_1=\begin{pmatrix}x \\ y \\ z\...
 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  python
python  python
python  python
python  python
python  python
python  python
python  python
python  python
python 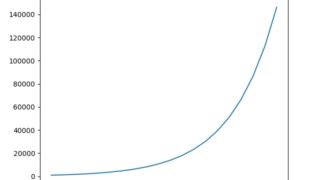 python
python 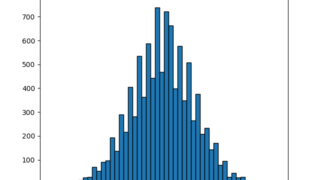 python
python 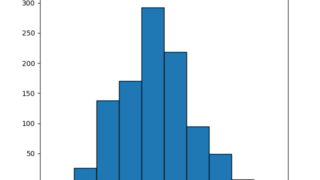 python
python  python
python