サイコロと中心極限定理

サイコロのある面が出る確率はどの目でも一様であると考えれば

$$\begin{align} P(X)=\frac{1}{6} \end{align}$$

となる。いまサイコロを $N$ 回振り、その平均を求めることを考える。

例えばサイコロのある面の出る期待値は

$$\begin{align} E(X)=\frac{7}{2} \end{align}$$

であるから$N$回サイコロを振ればその合計は

$$\begin{align} \frac{7N}{2} \end{align}$$

となる可能性が高いと考えられる。今回は数が大きくなるので出目の平均を計算しその頻度を描画する。

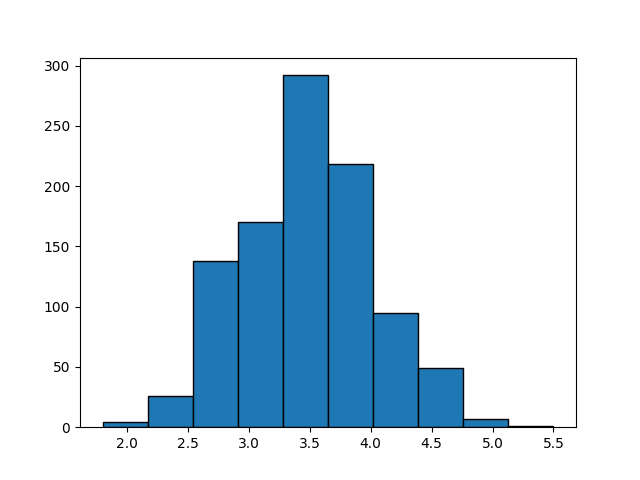
試行回数が増えるほどに正規分布に近づく。