三角関数の近似式 ２

十分小さい正の角度\(\theta\)について、\(\cos \theta\)は\(\tan \theta \)を用いて

\begin{align}
\cos \theta \approx 1 – \frac{\tan^2 \theta}{2}
\end{align}

で近似できる。

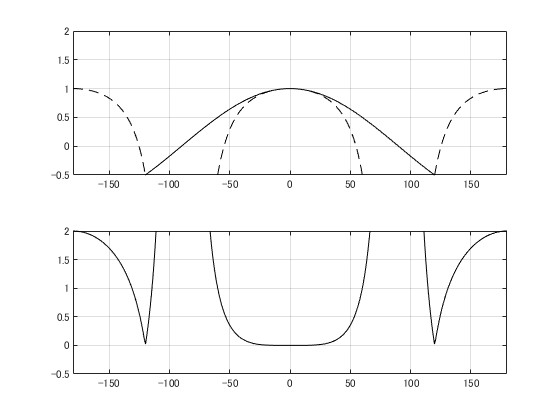
グラフは次のようになる。実線が\(\cos \theta \)、点線が\(1 – \frac{\tan^2 \theta}{2} \)。

下のグラフが誤差。分小さい正の角度\(\theta\)について近似できることが分かる。

ソースコード。MATLABで動く。sindとすればdegreeで角度指定できる。

t=linspace(-180,180,360);

figure;
subplot(2,1,1);
plot(t,cosd(t),'k');
hold on
plot(t,1-(tand(t).^2)./2,'k--');
grid on
ylim([-0.5, 2]);
xlim([-180,180]);

subplot(2,1,2);
plot(t,abs(cosd(t)-(1-tand(t).^2./2)),'k');
grid on
ylim([-0.5, 2]);
xlim([-180,180]);