共振角周波数と共振値

次のような二次遅れ系

$$\begin{align} G(s)=\dfrac{R(s)}{C(s)}=\dfrac{\omega_{n}^2}{s^2 + 2 \zeta \omega_{n} s+ \omega_{n}^2} \end{align}$$

の共振角周波数$\omega_{p}$ と共振値 $M_{p}$を求める。この系の伝達関数の周波数伝達関数$G(j \omega)$ は

$$\begin{align} G(j \omega)=\dfrac{1}{1+j 2 \zeta \left( \dfrac{\omega}{\omega_{n}} \right) – \left ( \dfrac{\omega}{\omega_{n}} \right)^2} \end{align}$$

ゲイン$M$は

$$\begin{align} M=\left | G(j \omega) \right | =\dfrac{1}{\sqrt{ \left \{ 1- \left( \dfrac{\omega}{\omega_{n}} \right )^2 \right \}^2 + \left \{ 2 \zeta \left ( \dfrac{\omega}{\omega_{n}} \right ) \right \}^2 }} \end{align}$$

ここで$u=\dfrac{\omega_{p}}{\omega_{n}}$とすると

$$\begin{align} M=\left | G(j \omega) \right | =\dfrac{1}{\sqrt{ \left \{ 1- u^2 \right \}^2 + \left ( 2 \zeta u \right )^2 }} \end{align}$$

を得る。この関数のグラフは$\zeta$を変化させ個々にプロットすれば

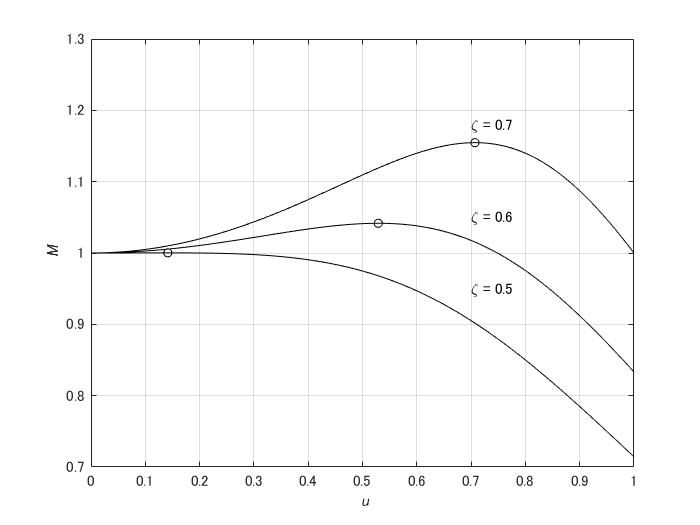
となる。丸の点は各グラフの最大値になっている。次にこのグラフの最大値を求める。最大値は

$$\begin{align} \dfrac{dM}{du}= u^2 – 1 + 2 \zeta^2=0 \end{align}$$

より

$$\begin{align} u= \sqrt{1 – 2 \zeta^{2}} \end{align}$$

最大値の時の$u$を$u_p$とすれば

$$\begin{align} u_{p}= \sqrt{1 – 2 \zeta^{2}}=\dfrac{\omega_{p}}{\omega_{n}} \end{align}$$

この時の$\omega$を共振角周波数といい$\omega_{p}$と置けば

$$\begin{align} \omega_{p}= \omega_{n} \sqrt{1 – 2 \zeta^{2}} \end{align}$$

また、この周波数が存在するには

$$\begin{align} 1 – 2 \zeta^{2} >0 \end{align}$$

となる必要が有るため$\zeta$は

$$\begin{align} \zeta < \dfrac{1}{\sqrt{2}} \end{align}$$

としなければならない。共振値$M_{p}$は$u=u_{p}$を代入して整理すれば

$$\begin{align} M_{p} = \dfrac{1}{2 \zeta \sqrt{1 – \zeta^2}} \end{align}$$

となる。