 MATLAB/simulink
MATLAB/simulink MATLABで素数の数を求める
これのMATLAB版n = 15;count = 0;for i = 1:n disp(); count = count + isprime(i);enddisp();function p = isprime(n) k = factoria...
 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  C/C++/C#
C/C++/C#  MATLAB/simulink
MATLAB/simulink  ChatGPT
ChatGPT  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C# 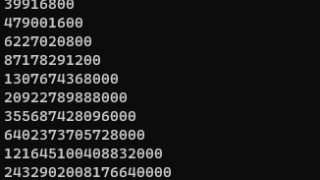 C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#