電流の関係式
\begin{align}
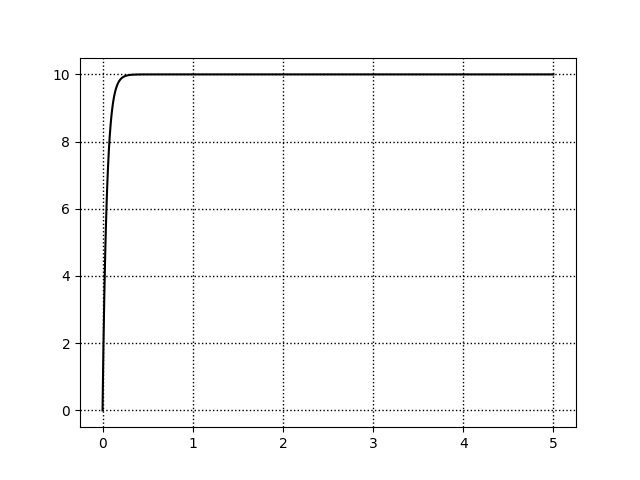
i=\frac{dq}{dt}= C \frac{dv}{dt}
\end{align}
より出力電圧は
\begin{align}
\frac{dv}{dt} = \frac{E-v}{CR}
\end{align}
これをルンゲクッタ法で解く。
ソース
import numpy as np
from matplotlib import pyplot as plt
def diff(x):
c = 470*10**-6
r = 100
e = 10
return (e - x) / (c * r)
def RungeKutta(x0,t0,tn,n):
x=np.zeros(n)
x[0] = x0
t = t0
h = (tn - t0) / n
for i in range(1,n):
t = t0 + i * h;
d1 = diff(x[i-1]);
d2 = diff(x[i-1] + d1 * h * 0.5);
d3 = diff(x[i-1] + d2 * h * 0.5);
d4 = diff(x[i-1] + d3 * h);
x[i] = x[i-1] + (d1 + 2 * d2 + 2 * d3 + d4) * (h / 6.0);
return x
x0=0
t0=0
t=5
n=1000
y = RungeKutta(x0, t0, t, n)
time=np.linspace(t0,t,n)
plt.figure(1)
plt.plot(time,y, 'k-')
plt.grid(color='k', linestyle='dotted', linewidth=1)
plt.show()
結果

コメント