3次式の因数分解と展開に関する公式について

今回は３次式の因数分解・展開公式が実際に成り立つか確認する。

まず

\begin{align}
x^3+y^3=(x+y)(x^2-xy+y^2)
\end{align}

については多項式の除法を使って

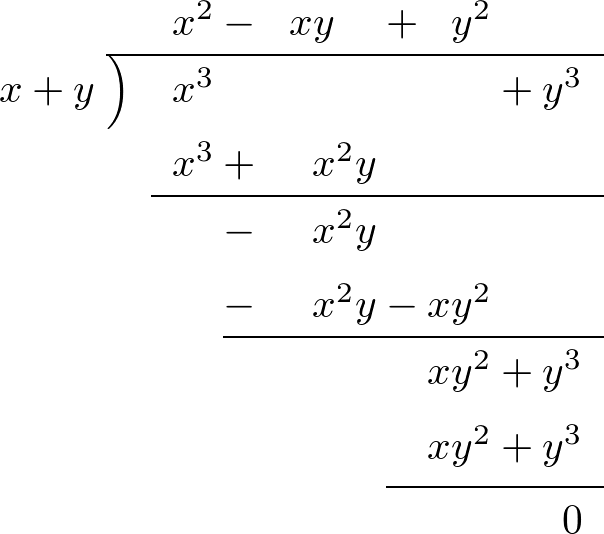
となる。

\begin{align}
x^3+3x^2y+3xy^2+y^3=(x+y)^3
\end{align}

は素直に展開して

\begin{align}
(x+y)^3&=(x+y)^2(x+y)\\
&=(x^2+2xy+y^3)(x+y)\\
&=x^3+3x^2y+3xy^2+y^3
\end{align}

となる。符号が異なっていても同様の手順で確認できるので試してみてほしい。

\begin{align}
x^3 +y^3&=(x + y)(x^2 – xy+y^2)\\
x^3 – y^3&=(x – y)(x^2 + xy+y^2)
\end{align}

\begin{align}
x^3 + 3x^2y+3xy^2+y^3&=(x + y)^3\\
x^3 – 3x^2y+3xy^2-y^3&=(x – y)^3
\end{align}