MATLAB/simulinkを使って簡単な適応制御を試す

一次遅れ系を例にMIT方式に基づくモデル規範型適応制御を試してみる。

今、制御対象を

\begin{align}
y(s)=\frac{b}{s+a}
\end{align}

で表す。これは微分方程式で書き直せば、

\begin{align}
\dot{y}(t) + ay(t) = bu(t)
\end{align}

となる。同様に規範モデル

\begin{align}
y_M(s)=\frac{b_M}{s+a_M}
\end{align}

を定義し、微分方程式で書き直せば

\begin{align}
\dot{y}_{M} (t) + a_{M} y(t) = br(t)
\end{align}

となる。

次にこの制御の目的は制御対象のゲインによる影響を適応的に補正し、制御対象の応答を規範モデルの応答と一致するようにすることである。したがって

\begin{align}
e(t)=y_{M}(t)-y(t) \to 0
\end{align}

制御入力は

\begin{align}
u(t) = \theta_1(t)r(t) + \theta_2(t)y(t)
\end{align}

で与える。

一方MIT方式によるパラメータの更新則は

\begin{align}
\dot{\theta_1}(t) = \alpha_1 \left (\frac{1}{s+a_M}r(t) \right ) e(t)\\
\dot{\theta_2}(t) = \alpha_2 \left (\frac{1}{s+a_M}y(t) \right ) e(t)
\end{align}

で与えられる。

これをsimulinkで表現すれば

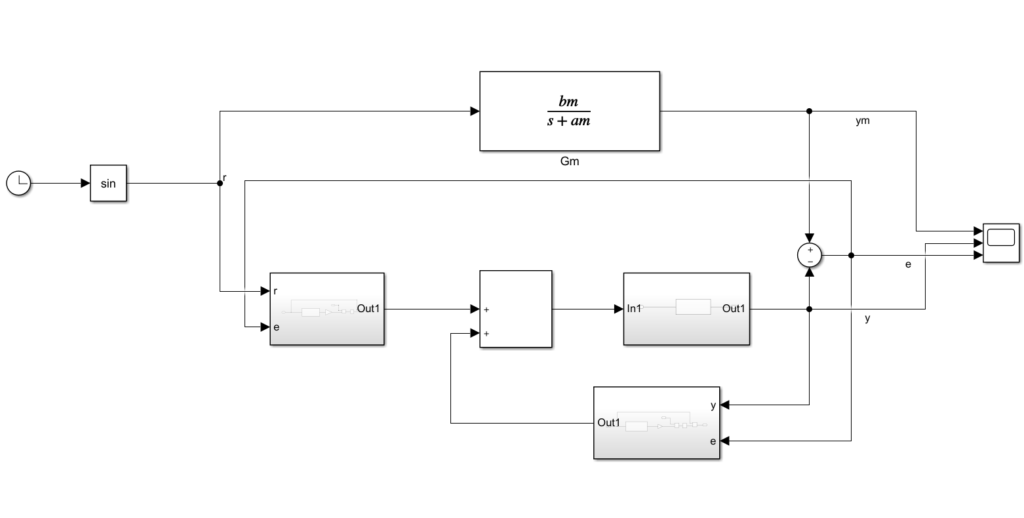
となり、出力は

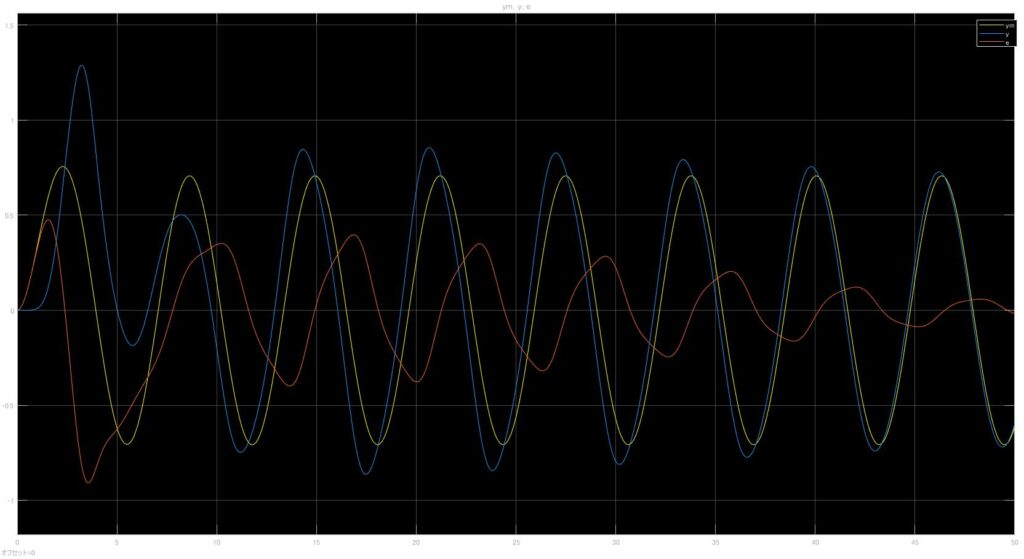
となった。

正しく動作していそうであれば、後日詳しい記事を書こうと思う。