指定した極を実現する伝達関数を求める

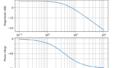
二次遅れ系

\begin{align}
P(s)=\frac{\omega_{n}^2 }{s^2 + 2 \zeta \omega_{n} s + \omega_{n}^2}
\end{align}

に極が与えられたとき、その極を実現する伝達関数を導出する。

今極に\(p=-5\pm j \)が与えられているとき

\begin{align}
s=- \omega_n \zeta \pm \omega_n \sqrt{\zeta^2-1}
\end{align}

より

\begin{align}
\omega_n = \sqrt{26}, \zeta =5
\end{align}

となり

\begin{align}
P(s)=\frac{ 26 }{s^2 + 10 s + 26}
\end{align}

を得る。