Pythonでフィードバック結合のシミュレーションをする。
\begin{align}
P(s)=\frac{\omega_{n}^2 }{s^2 + 2 \zeta \omega_{n} s + \omega_{n}^2}
\end{align}
PID制御則
\begin{align}
C(s)=K_{P} + \frac{K_{I}}{s}+K_{D} s
\end{align}
を行った場合の伝達関数
\begin{align}
G(s)=\frac{P (s)C(s) }{1+P(s) C(s) }
\end{align}
をシミュレーションする。
コードは以下
from control.matlab import *
import matplotlib.pyplot as plt
s = tf('s')
Kp = 2.5
Ki = 0.75
Kd = 0.75
zeta = 0.5
omega = 1
C = Kp + Ki / s + Kd * s
P = omega ** 2 / (s ** 2 + 2 * zeta * omega * s + omega ** 2)
G = feedback(C * P, 1)
t, y = step(G)
plt.plot(y, t, 'k-')
plt.grid(color='k', linestyle='dotted', linewidth=1)
plt.show()
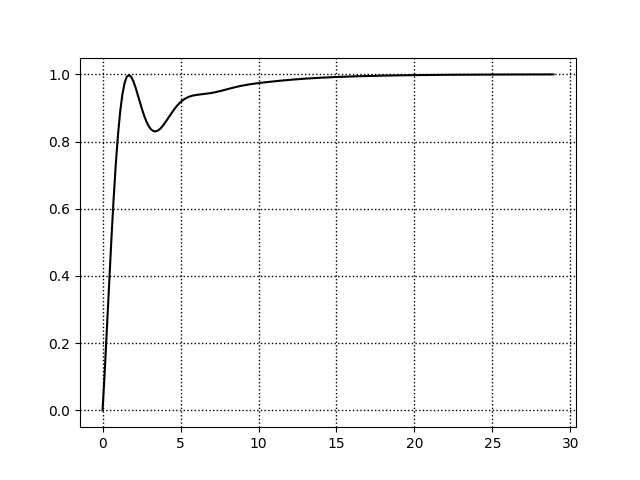

コメント