ナイキスト線図を使えば複雑なシステムの安定判別をより容易に行えるようになる場合がある。今回は細かいことを気にせずただナイキスト線図を描画する。正しく描けているかのチェックにはMATLABの関数「nyquist」を使用した。
いま開ループ伝達関数が
\begin{align}
G(s) =\frac{2s^2+5s+1}{s^2+2s+3}
\end{align}
で与えられているとする。ナイキスト線図を書くには\(s=j \omega\)を代入し、\(\omega\)を変化させればいい。つまり
\begin{align}
G(j \omega) =\frac{2(j \omega)^2+5(j \omega)+1}{(j \omega)^2+2(j \omega)+3}
\end{align}
これを計算してプロットした結果がこちら
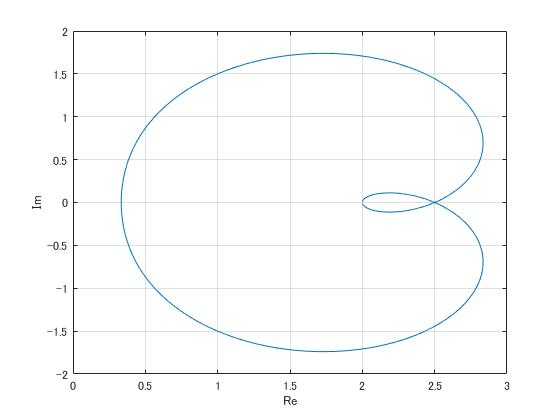
「nyquist」で描画したときと同様の結果が得られた。
MATLABコードはこちら
s=tf('s');
G =(2*s^2+5*s+1)/(s^2+2*s+3);
nyquist(G)
j=sqrt(-1);
omega=-100:0.001:100;
G =(2*(j*omega).^2+5*(j*omega)+1)./((j*omega).^2+2.*(j*omega)+3);
figure;
plot(G)
xlabel('Re');
ylabel('Im');
grid on




コメント