これの続き。忘却係数付き逐次最小二乗法の更新則は
\begin{align}
\hat{\theta}_{N} &= \hat{\theta}_{N-1} + \dfrac{P_{N-1} z_{N} }{\rho + z_{N}^{T} P_{N-1} z_{N}} \left ( y_{N} – z_{i}^{T} \hat{\theta}_{N-1} \right) \\[1.5ex]
P_{N} &= \frac{1}{\rho} \left ( P_{N-1} – \dfrac{P_{N-1} z_{N} z_{N}^{T} P_{N-1}}{\rho + z_{N}^{T} P_{N-1} z_{N}} \right)
\end{align}
であるのでこれをPythonで実装すると次のようになる。
from control.matlab import *
import numpy as np
from matplotlib import pyplot as plt
def rls(theta_, pn_, rn_, yn, zn):
trzn = np.reshape(zn, (1, 4))
rls_num = rn_ + trzn @ pn_ @ zn
pn = 1 / rn_ * (pn_ - (pn_ @ zn @ trzn @ pn_) / rls_num)
ln = (pn_ @ zn) / rls_num
en = yn - trzn @ theta_
theta = theta_ + ln * en
return theta, pn
N = 1000
t = np.linspace(0, 10, N)
alpha = 1000
Pn = alpha * np.eye(4)
est = np.zeros((N, 4))
Theta = np.reshape(np.zeros(4), (4, 1))
s = tf('s')
omega=1
zeta=0.1
P = omega ** 2/(s ** 2 + 2 * zeta * omega * s + omega ** 2)
G=feedback(P,1)
r = np.zeros(N)
r[0:100] = 1
a1 = np.zeros(N)
a2 = np.zeros(N)
b1 = np.zeros(N)
b2 = np.zeros(N)
y, t, x = lsim(G, r, t)
plt.figure(1)
plt.plot(t, y, 'k-')
plt.grid(color='k', linestyle='dotted', linewidth=1)
for i in range(2, N):
Yn = y[i]
trZn = np.array([-y[i - 1], -y[i - 2], r[i - 1], r[i - 2]])
Zn = np.reshape(trZn, (4, 1))
Theta, Pn = rls(Theta, Pn, 0.98, Yn, Zn)
a1[i] = Theta[0]
a2[i] = Theta[1]
b1[i] = Theta[2]
b2[i] = Theta[3]
plt.figure(2)
plt.plot(t, a1, 'k-')
plt.grid(color='k', linestyle='dotted', linewidth=1)
plt.plot(t, a2, 'k-')
plt.grid(color='k', linestyle='dotted', linewidth=1)
plt.plot(t, b1, 'k-')
plt.grid(color='k', linestyle='dotted', linewidth=1)
plt.plot(t, b2, 'k-')
plt.grid(color='k', linestyle='dotted', linewidth=1)
Hnum = [b1[N-1], b2[N-1]]
Hden = [1 , a1[N-1], a2[N-1]]
H = tf(Hnum, Hden, 1/N)
yH, tH, xH = lsim(H, r)
plt.figure(3)
plt.plot(tH, yH, 'k-')
plt.grid(color='k', linestyle='dotted', linewidth=1)
plt.show()
結果
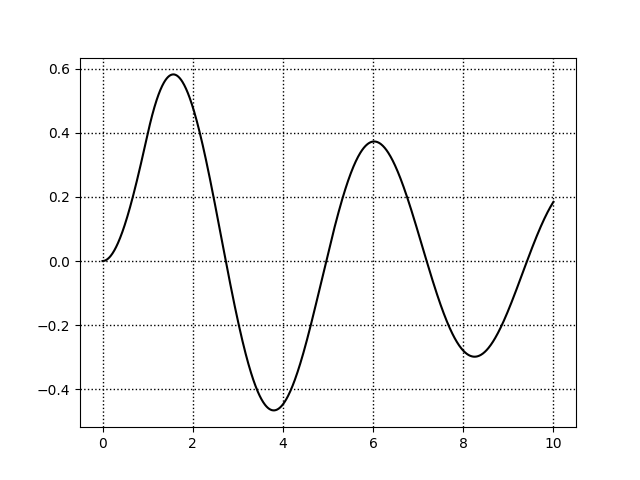
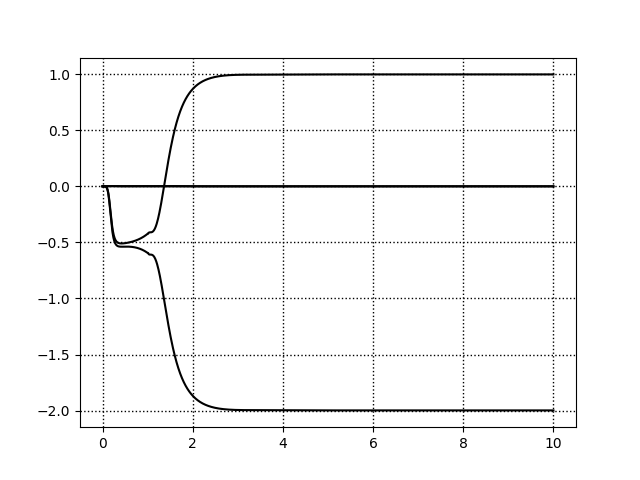

コメント