次のような二次遅れ系の伝達関数\(G(s)\)
\begin{align}
G(s)=\dfrac{\omega_{n}^2}{s^2 + 2 \zeta \omega_{n} s+ \omega_{n}^2}
\end{align}
について、インパルス応答を調べる。インパルス応答を入力したときの出力\(Y(s)\)は
\begin{align}
p_{1},p_{2}= \left ( – \zeta \pm \sqrt{\zeta^2-1} \right ) \omega_{n}
\end{align}
\begin{align}
Y(s)=\dfrac{\omega_{n}^2}{s^2 + 2 \zeta \omega_{n} s+ \omega_{n}^2}
\end{align}
で与えられる。\(Y(s)\)の極を\(p_{1},p_{2}\)とすれば
・\(\zeta >1\)のとき
\(Y(s)\)について
\begin{align}
Y(s)=\frac{A}{s-p_{1}}+\frac{A}{s-p_{2}}
\end{align}
と部分分数分解すると
\begin{align}
Y(s)=\frac{\omega_{n} }{ 2 \sqrt{\zeta^2 – 1 } } \left ( \frac{1}{s-p_{1}} – \frac{1}{s-p_{2}} \right )
\end{align}
逆ラプラス変換して
\begin{align}
y(t) &=\frac{\omega_{n} }{ 2 \sqrt{\zeta^2 – 1 } } \left ( e^{p_{1} t} – e^{p_{2} t} \right ) \\
&= \frac{\omega_{n} }{ 2 \sqrt{\zeta^2 – 1 } } e^{- \zeta \omega_{n} } \left ( e^{ \omega_{n} \sqrt{\zeta^2 -1 } t} – e^{- \omega_{n} \sqrt{\zeta^2 -1 }t } \right )
\end{align}
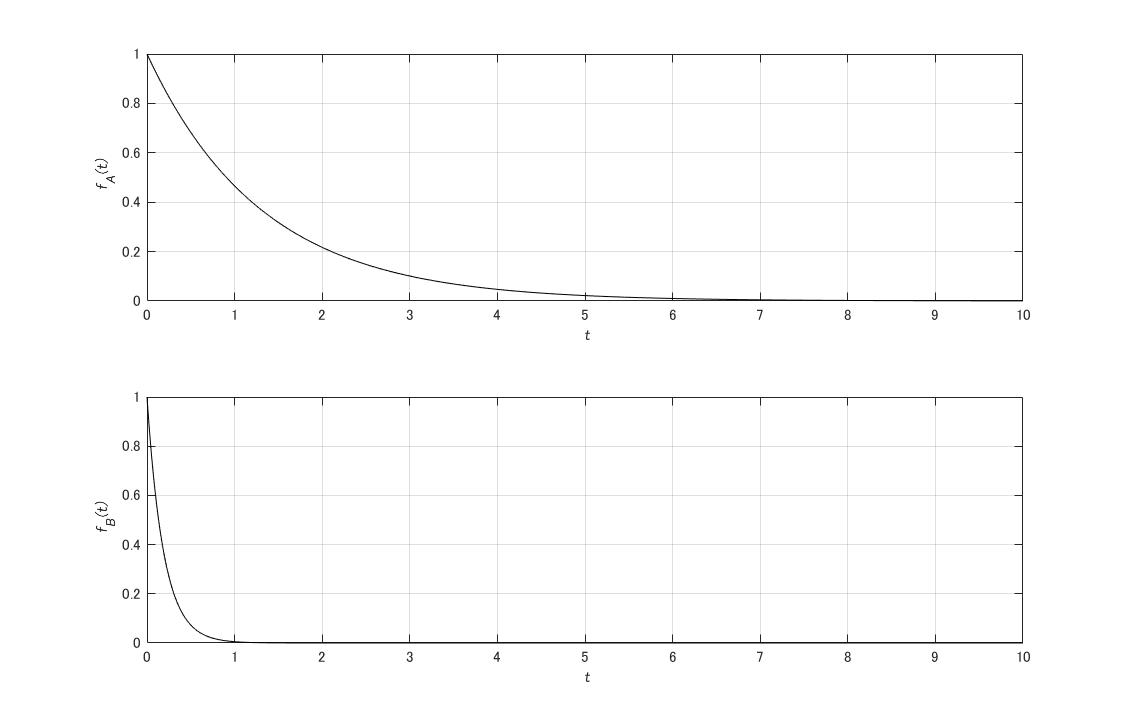
ここで\(f_{A}(t),f_{B}(t)\)を
\begin{align}
f_{A}(t) =e^{ \omega_{n} \sqrt{\zeta^2 -1 } t} \hspace{10mm} f_{B}(t) = e^{- \omega_{n} \sqrt{\zeta^2 -1 }t }
\end{align}
\(\zeta=1.5,\omega_{n}=2\)としてグラフを書けば
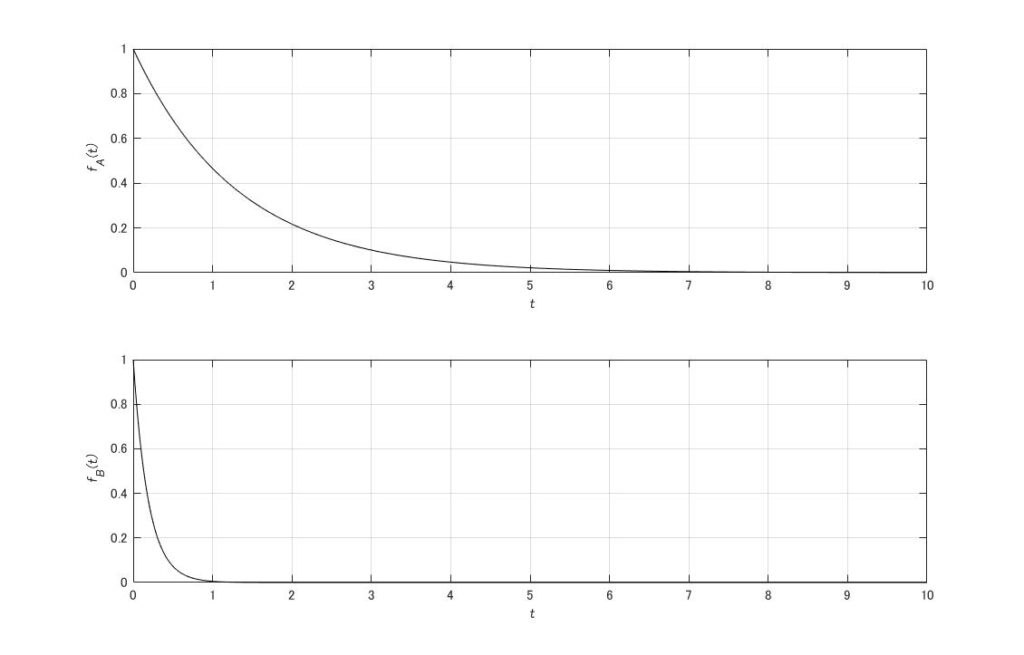
となることから\(f_{A}(t)\)の方が減衰が緩やかになる。
最後に応答は
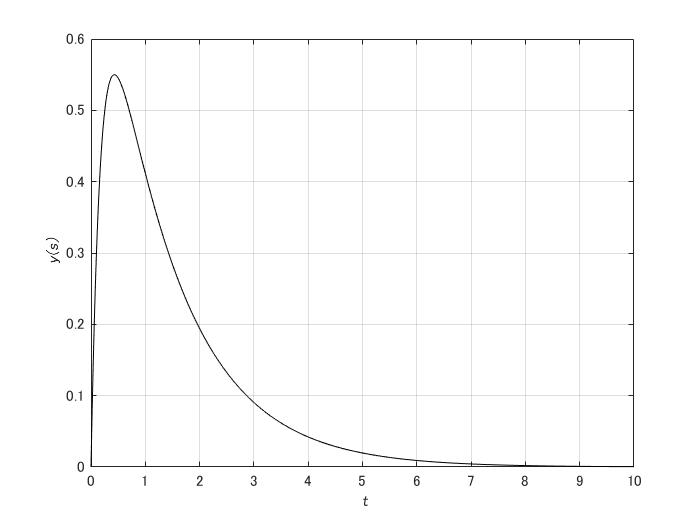
・\(\zeta=1\)のとき
\begin{align}
p_{1}=p_{2}=-\omega_{n}
\end{align}
より
\begin{align}
Y(s)=\frac{\omega_{n}^2 } { \left ( s + \omega_{n} \right )^2}
\end{align}
逆ラプラス変換すれば
\begin{align}
y(t)=\left ( t e^{ – \omega_{n} t} \right ) \omega_{n}^2
\end{align}
\(\zeta=1,\omega_{n}=2\)としてグラフを書けば
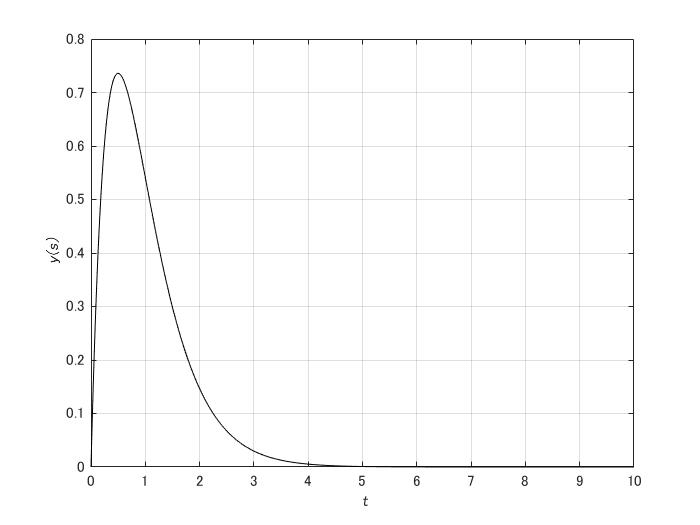
・\(0<\zeta < 1\)のとき
\begin{align}
p_{1},p_{2}= \left ( – \zeta \pm j \sqrt{1 – \zeta^2} \right ) \omega_{n}
\end{align}
よって
\begin{align}
y(s)=\frac{\omega_{n}^{2}}{\sqrt{1-\zeta^2}} e^{- \omega_{n} t} \sin \sqrt{1-\zeta^2} t
\end{align}
\(\zeta=0.6,\omega_{n}=2\)としてグラフを書けば
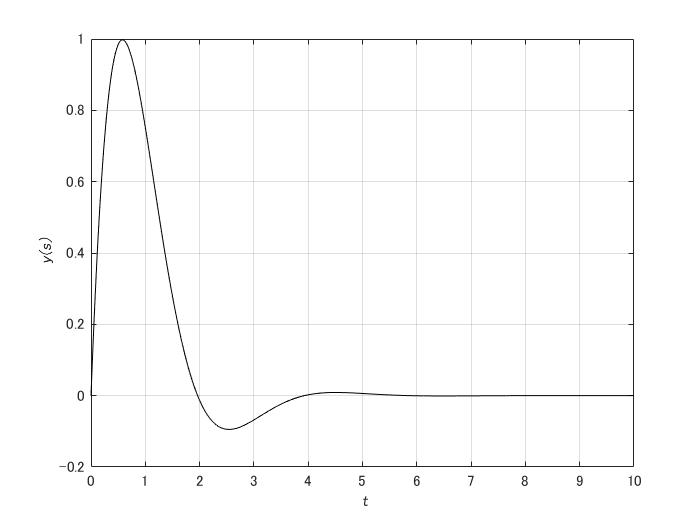
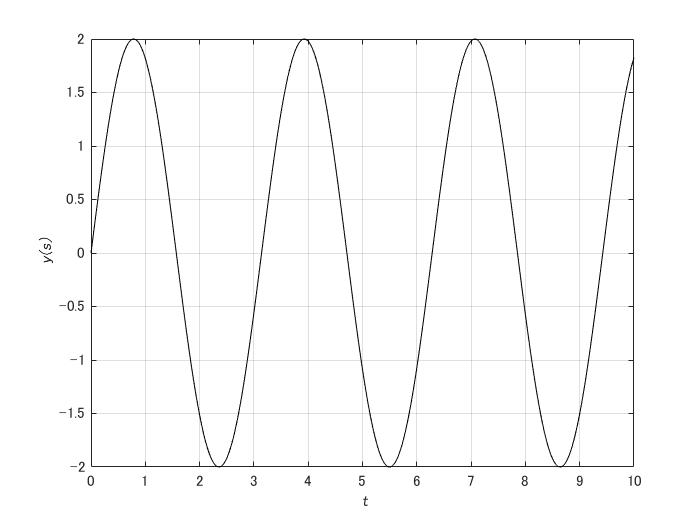
・\(\zeta=0\)のとき
\begin{align}
Y(s) = \frac{\omega_{n}^2}{s^2 + \omega_{n}^2}
\end{align}
よって
\begin{align}
y(s)= \omega_{n} \sin \omega_{n} t
\end{align}
\(\zeta=0,\omega_{n}=2\)としてグラフを書けば


コメント