一次遅れ系の伝達関数
\begin{align}
G=\frac{K}{Ts+1}
\end{align}
について、係数の持つ意味を理解する。一般に\(K\)は比例ゲイン、\(T\)は時定数と呼ばれる。
次のグラフは比例ゲインを固定し、時定数を変化させたときの様子をプロットしたものである。システムへはすべて単位ステップ関数を入力している。
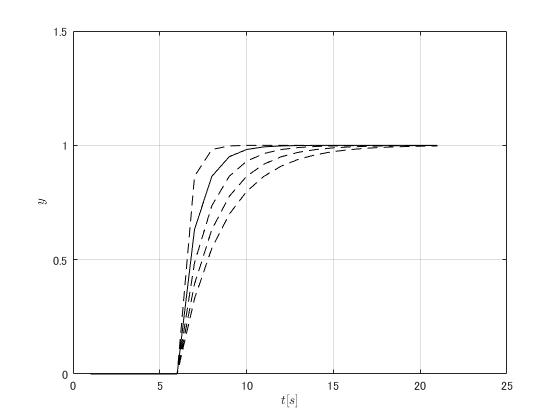
時定数が大きくなるにつれ、目標値へ到達する時間は遅くなる。
次に時定数を固定し、比例ゲインを変化させる。
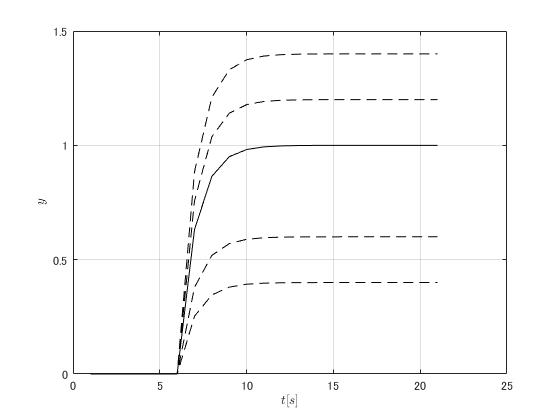
比例ゲインが大きくなるに従いグラフの最大値も増加している。時定数が変化していないので立ち上がりに必要な時間は変化していない。
このグラフは次のMATLABのソースで確認できる。
s=tf('s');
T=1;
K=1;
Tllist=[0.5 1.5 2.0 2.5]';
Kllist=[0.4 0.6 1 1.2 1.4]' ;
G=K/(T*s+1);
t=0:1:20;
r=zeros(21,1);
r(6:21,1)=1;
y=lsim(G,r,t);
figure;
plot(y,'k')
xlim([0 25]);
ylim([0 1.5]);
xlabel('$t$[$s$]','Interpreter', 'latex');
ylabel('$y$','Interpreter', 'latex');
grid on
hold on
for i=1:1:length(Tllist)
T=Tllist(i,1);
G=K/(T*s+1);
y=lsim(G,r,t);
plot(y,'k--')
hold on
end
T=1;
G=K/(T*s+1);
y=lsim(G,r,t);
figure;
plot(y,'k')
xlim([0 25]);
ylim([0 1.5]);
xlabel('$t$[$s$]','Interpreter', 'latex');
ylabel('$y$','Interpreter', 'latex');
grid on
hold on
for i=1:1:length(Kllist)
K=Kllist(i,1);
G=K/(T*s+1);
y=lsim(G,r,t);
plot(y,'k--')
hold on
end
次は二次遅れ系についても同様に調べる。

コメント