大学入学共通テスト2023のIIBの問1(1)

問１(1)

\(x=\frac{\pi}{6}\)のとき\(\sin x □ \sin 2x\)であり、\(x=\frac{2}{3} \pi\)のとき\(\sin x □ \sin 2x\)である。

この問題は□に大小関係を補う問題である。\(\sin 2x\)は\(\sin x\)の倍の周波数を持つ。これはグラフで容易に確認できる。

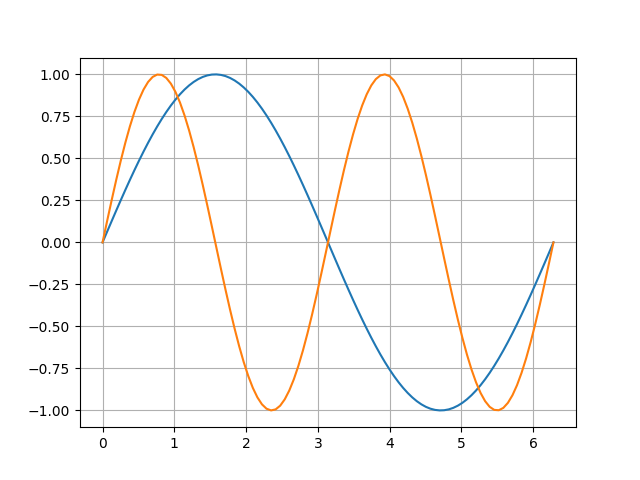
ソース

import numpy as np
import matplotlib.pyplot as plt

theta = np.linspace(0, 2 * np.pi, 100)

P1 = np.sin(theta)
P2 = np.sin(2*theta)

plt.plot(theta, P1, label="test")
plt.plot(theta, P2, label="test")

plt.grid()
plt.show()

愚直に計算すれば

・\(x=\frac{\pi}{6}\)のとき

\begin{align}
\sin \frac{\pi}{6} &= \frac{1}{2}\\
\sin 2 \times \frac{\pi}{6} &=\sin \frac{\pi}{3} = \frac{\sqrt{3}}{2}
\end{align}

より\(\sin x < \sin 2x\)

・\(x=\frac{2}{3} \pi\)のとき

\begin{align}
\sin \frac{2}{3}\pi &= \frac{\sqrt{3}}{2}\\
\sin 2 \times \frac{2}{3}\pi &=\sin \frac{4}{3}\pi= -\frac{\sqrt{3}}{2}
\end{align}

より\(\sin x > \sin 2x\)

なお、\(\pi=180\)を代入すればDegreeに変換でき

\begin{align}
\frac{180}{6}[rad] &= 30[度]\\
\frac{2}{3} \times 180 [rad]&=120[度]
\end{align}